Введите слово или словосочетание на любом языке 👆
Язык:
Перевод и анализ слов искусственным интеллектом ChatGPT
На этой странице Вы можете получить подробный анализ слова или словосочетания, произведенный с помощью лучшей на сегодняшний день технологии искусственного интеллекта:
- как употребляется слово
- частота употребления
- используется оно чаще в устной или письменной речи
- варианты перевода слова
- примеры употребления (несколько фраз с переводом)
- этимология
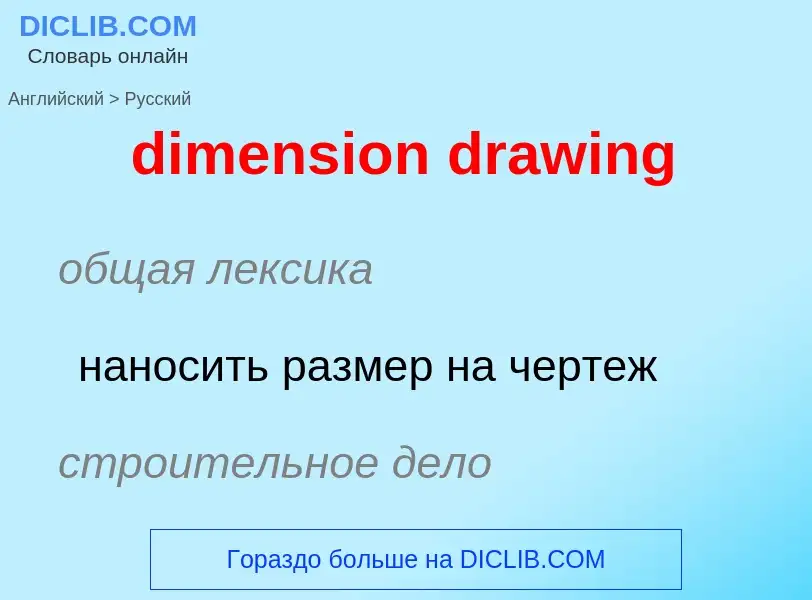
dimension drawing - перевод на русский
WIKIMEDIA DISAMBIGUATION PAGE
5th Dimension; 5Th Dimension; Fifth dimension (disambiguation); Fith Dimension; 5th dimension; Fifth dimension; Fifth Dimension (disambiguation)
dimension drawing
общая лексика
наносить размер на чертеж
строительное дело
чертёж с размерами
dimension drawing
чертёж с размерами
drawing
VISUAL ARTWORK IN TWO-DIMENSIONAL MEDIUM
Disegno; Drawings; Pen-and-ink drawing; Layout drawing; Outline drawing; History of drawing; How to Draw; Drawer (artist); Freehand drawing
1) чертёж; рисунок; эскиз
2) черчение
3) вытяжка (металла)
Определение
Размерность
I
Разме́рность (число измерений)
геометрической фигуры, число, равное единице, если фигура есть линия; равное двум, если фигура есть поверхность; равное трём, если фигура представляет собой тело. С точки зрения аналитической геометрии Р. фигуры равна числу координат, нужных для определения положения лежащей на этой фигуре точки; например, положение точки на кривой определяется одной координатой, на поверхности - двумя координатами, в трёхмерном пространстве - тремя координатами. Геометрия до середины 19 в. занималась только фигурами первых трёх Р. С развитием в середине 19 в. понятия о многомерном пространстве (См. Многомерное пространство) геометрия начинает заниматься фигурами любой Р. Простейшими фигурами размерности m являются m-мерные многообразия (См. Многообразие); m-мерное многообразие, расположенное в n-меpном пространстве, задаётся при помощи n - m уравнений (например, линия, т. е. одномерное многообразие, в трёхмерном пространстве задаётся 3 - 1 = 2 уравнениями). Положение точки на m-мерном многообразии определяется "криволинейными" координатами (например, положение точки на сфере определяется её "географическими координатами" - долготой и широтой; аналогично на торе). Приведённые выше положения справедливы лишь при некоторых ограничительных предположениях. Действительно общее определение Р. любого замкнутого ограниченного множества, лежащего в n-mepном евклидовом пространстве, было дано П. С. Урысоном: оказывается, для того чтобы такое множество имело размерность ≤ m, необходимо и достаточно, чтобы оно при любом ε > 0 допускало ε-Покрытие (замкнутыми множествами, имеющими кратность ≤ n + 1). Приведённое выше общее определение Р. допускает естественное обобщение на очень широкие классы топологических пространств (См. Топологическое пространство). Урысон построил в 1921 теорию Р. - одну из глубоких теорий современной топологии. Своим дальнейшим развитием теория Р. обязана главным образом советским математикам (П. С. Александров, Л. С. Понтрягин и др.).
Лит.: Александров П. С., Пасынков Б. А., Введение в теорию размерности, М., 1973.
II
Разме́рность
физической величины, выражение, показывающее, во сколько раз изменится единица физической величины при изменении единиц величин, принятых в данной системе за основные. Р. представляет собой одночлен, составленный из произведения обобщённых символов основных единиц в различных (целых или дробных, положительных или отрицательных) степенях, которые называются показателями Р. Так, например, Р. скорости LT-1, где Т представляет собой Р. времени, а L - Р. длины. Эти символы обозначают единицы времени и длины независимо от их конкретного размера (секунда, минута, час, метр, сантиметр и т.д.). В ряде случаев Р. позволяет устанавливать связи между соответствующими величинами (подробнее см. Размерностей анализ).
Википедия
Fifth Dimension
Fifth Dimension or fifth dimension may refer to:
- Five-dimensional space, a mathematical concept or construct
- The 5th Dimension, a pop music vocal group debuting in the 1960s
- 5th Dimension (album), a 2013 album by Momoiro Clover Z
- Fifth Dimension (album), a 1966 album by the Byrds
- "5D (Fifth Dimension)", a 1966 song by the Byrds
- Fifth Dimension, a program in the Radio Tales series for National Public Radio
- The 5th Dimension, the fictional home dimension of DC Comics villain Mister Mxyzptlk
- The 5th Dimension (ride), an amusement park ride
.jpg?width=200)
![A pencil portrait by [[Henry Macbeth-Raeburn]], with hatching and shading (1909) A pencil portrait by [[Henry Macbeth-Raeburn]], with hatching and shading (1909)](https://commons.wikimedia.org/wiki/Special:FilePath/Edward Law. Pencil drawing by H. M. Raeburn, 1909. Wellcome V0003431.jpg?width=200)
![[[Galileo Galilei]], ''Phases of the Moon'', 1609 or 1610, brown ink and wash on paper. 208 × 142 mm. [[National Central Library (Florence)]], Gal. 48, fol. 28r [[Galileo Galilei]], ''Phases of the Moon'', 1609 or 1610, brown ink and wash on paper. 208 × 142 mm. [[National Central Library (Florence)]], Gal. 48, fol. 28r](https://commons.wikimedia.org/wiki/Special:FilePath/Galileo moon phases.jpg?width=200)
![''Madame Palmyre with Her Dog'', 1897. [[Henri de Toulouse-Lautrec]] ''Madame Palmyre with Her Dog'', 1897. [[Henri de Toulouse-Lautrec]]](https://commons.wikimedia.org/wiki/Special:FilePath/Henri de Toulouse-Lautrec - Madame Palmyre with Her Dog, 1897.jpg?width=200)
![Drawing process in the ''Academic Study of a Male Torso'' by [[Jean-Auguste-Dominique Ingres]] (1801, [[National Museum, Warsaw]]) Drawing process in the ''Academic Study of a Male Torso'' by [[Jean-Auguste-Dominique Ingres]] (1801, [[National Museum, Warsaw]])](https://commons.wikimedia.org/wiki/Special:FilePath/Ingres Academic Study (detail) 03.jpg?width=200)
![worm's-eye perspective]] worm's-eye perspective]]](https://commons.wikimedia.org/wiki/Special:FilePath/Joeri Van Royen.jpg?width=200)

![A young woman drawing the [[Barberini Faun]] in [[Munich]] A young woman drawing the [[Barberini Faun]] in [[Munich]]](https://commons.wikimedia.org/wiki/Special:FilePath/Munich - Two young women drawing - 5814.jpg?width=200)
![[[Raphael]], study for what became the ''[[Alba Madonna]]'', with other sketches [[Raphael]], study for what became the ''[[Alba Madonna]]'', with other sketches](https://commons.wikimedia.org/wiki/Special:FilePath/Raphaël - Étude Madone d'Albe 1.jpg?width=200)

![[[Antoine Watteau]], ''[[trois crayons]]'' technique [[Antoine Watteau]], ''[[trois crayons]]'' technique](https://commons.wikimedia.org/wiki/Special:FilePath/Watteau jeune fille.jpg?width=200)
![study drawing]] by [[William-Adolphe Bouguereau]] study drawing]] by [[William-Adolphe Bouguereau]]](https://commons.wikimedia.org/wiki/Special:FilePath/William-Adolphe Bouguereau (1825-1905) - Study of a Seated Veiled Female Figure (19th Century).png?width=200)
